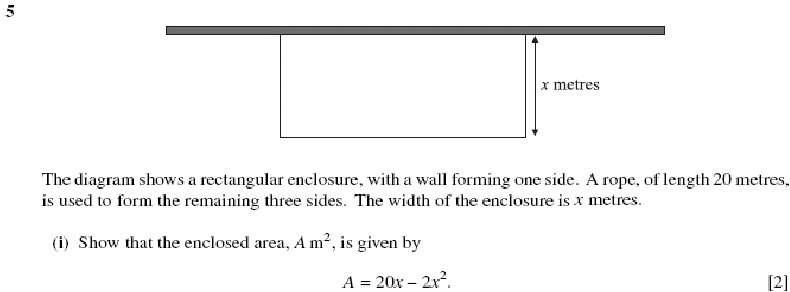
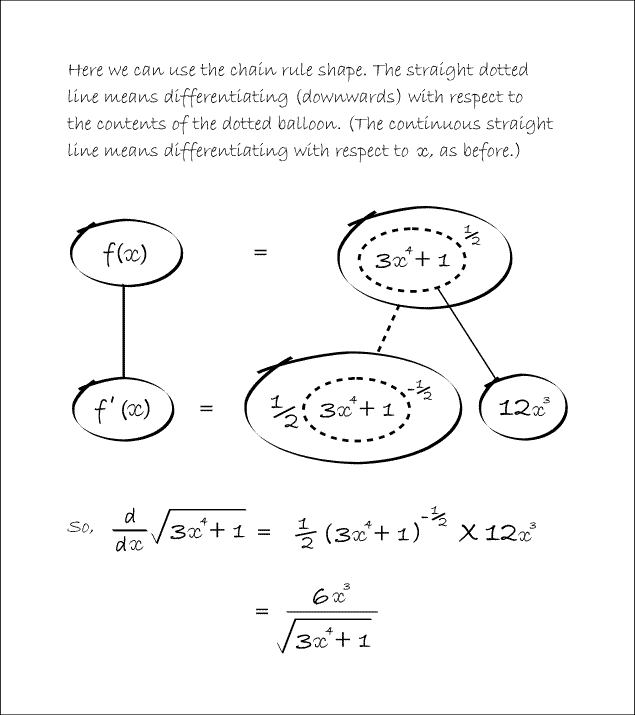
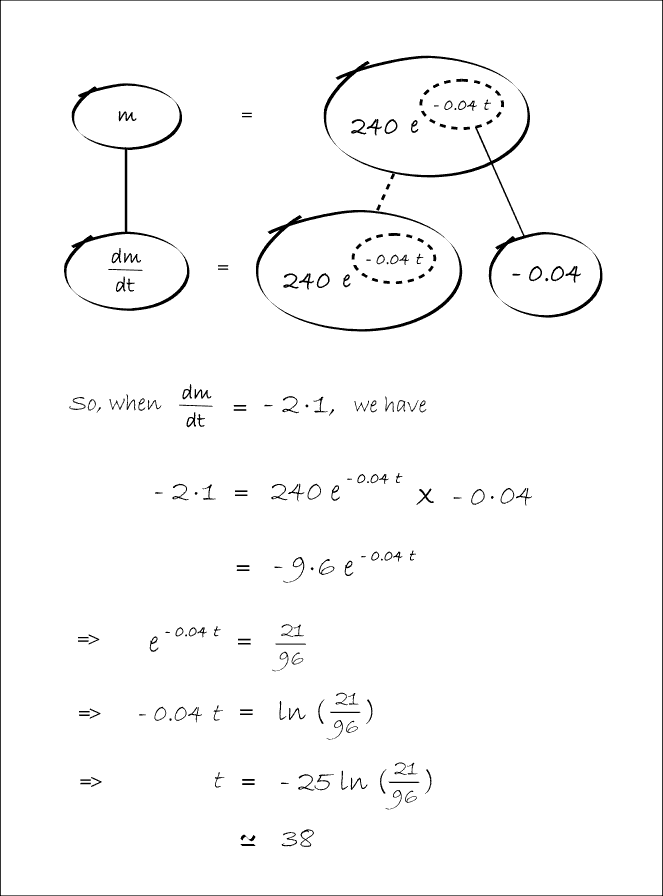
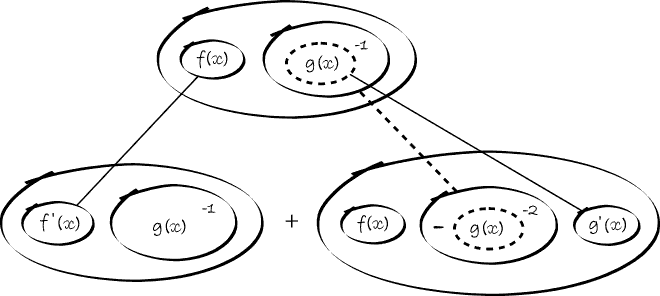
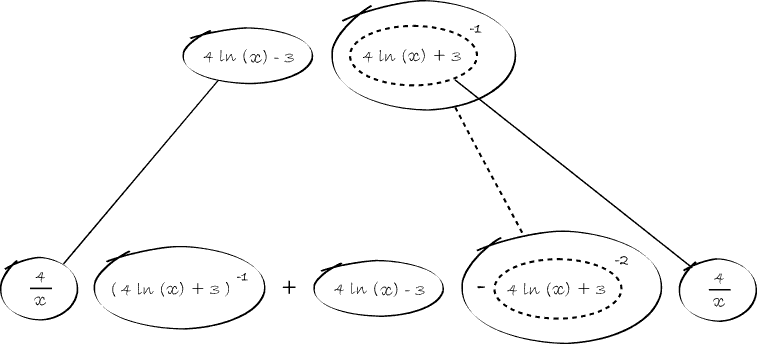
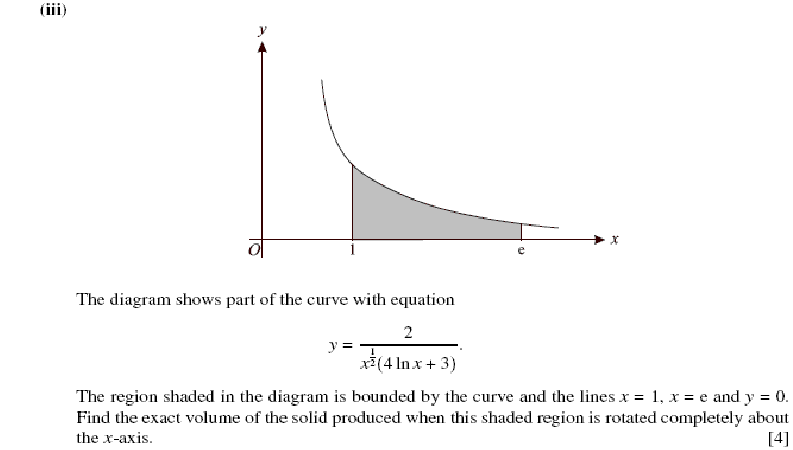
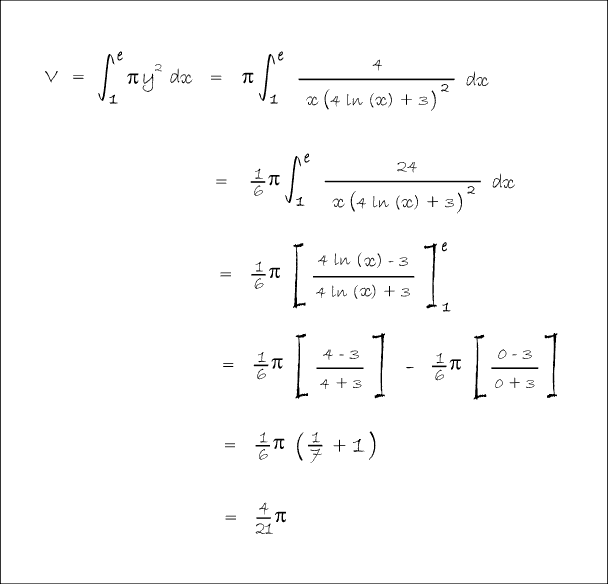
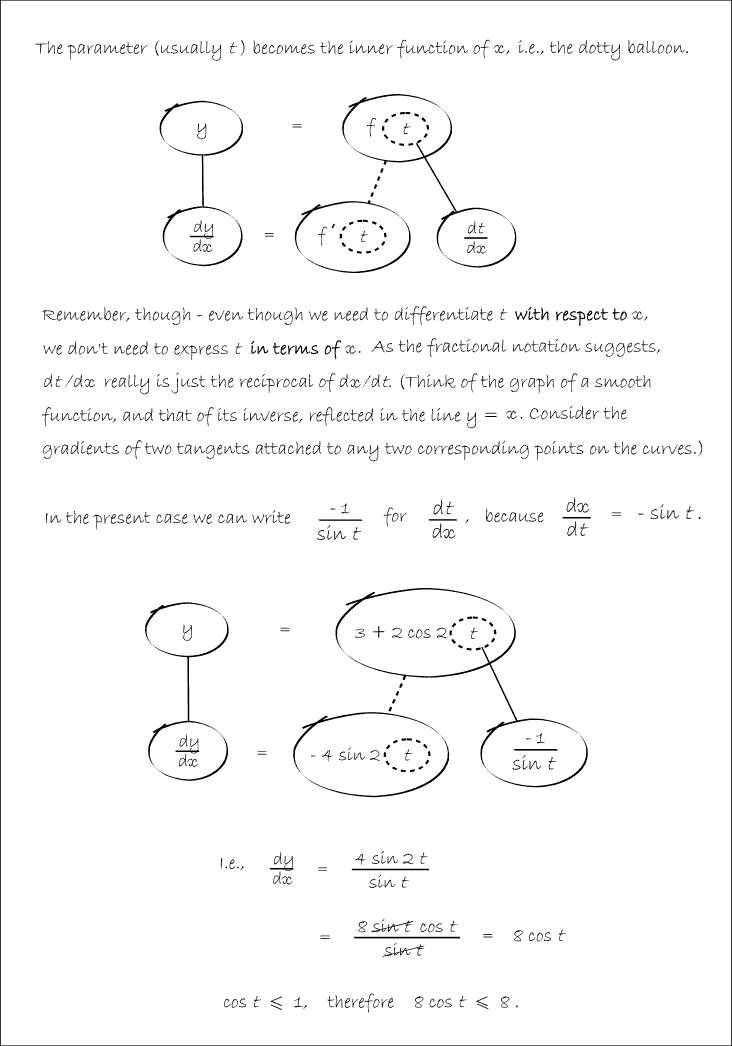
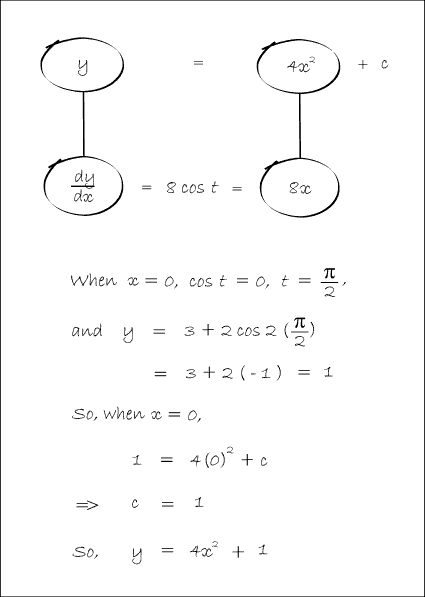
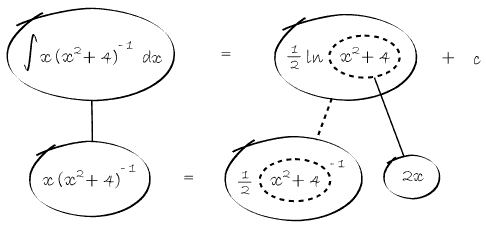
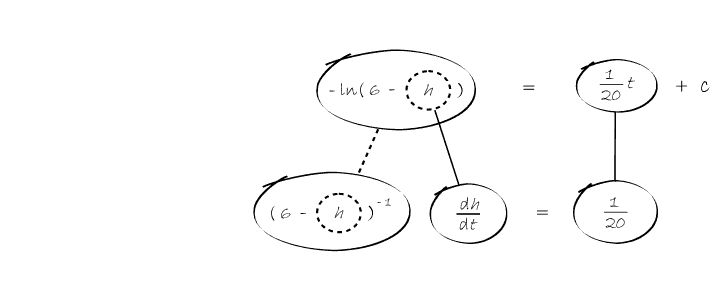
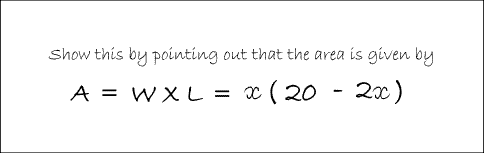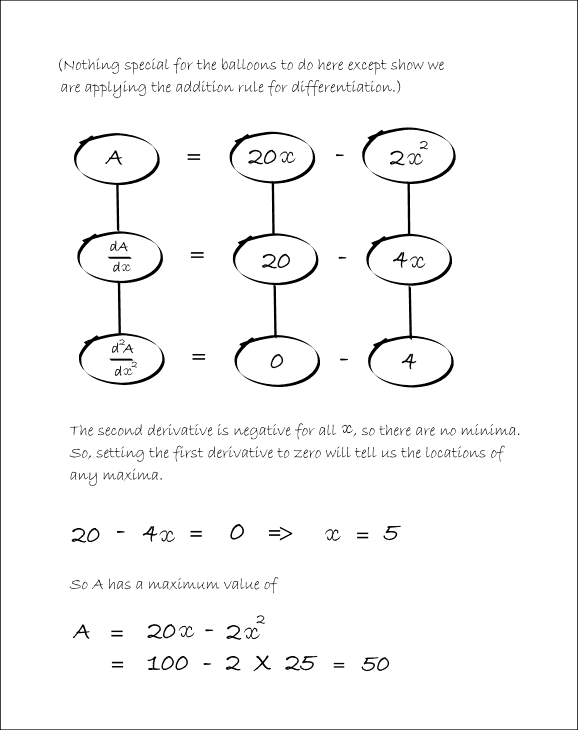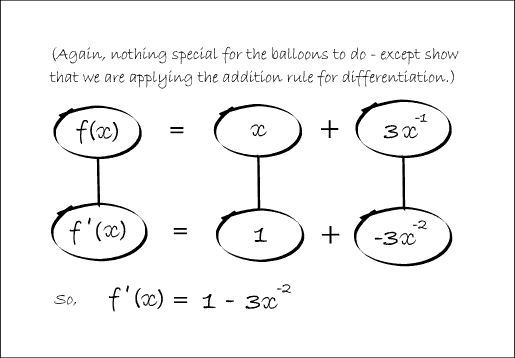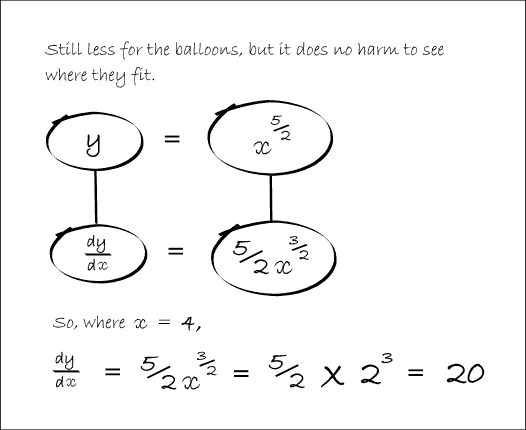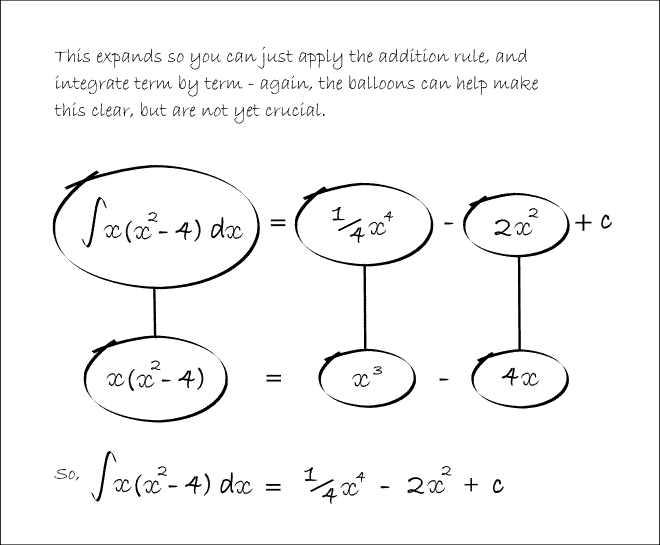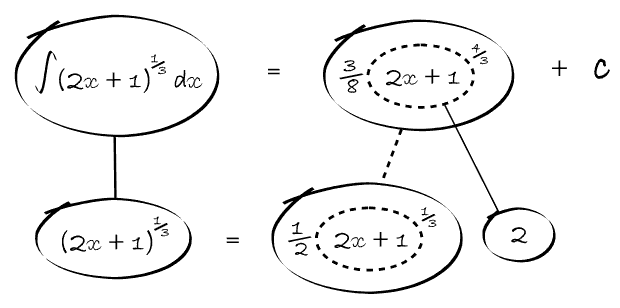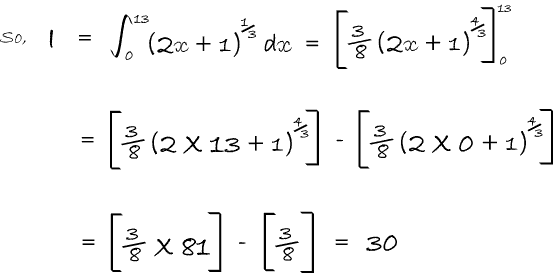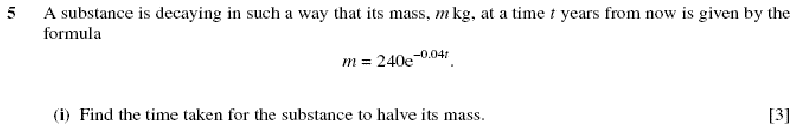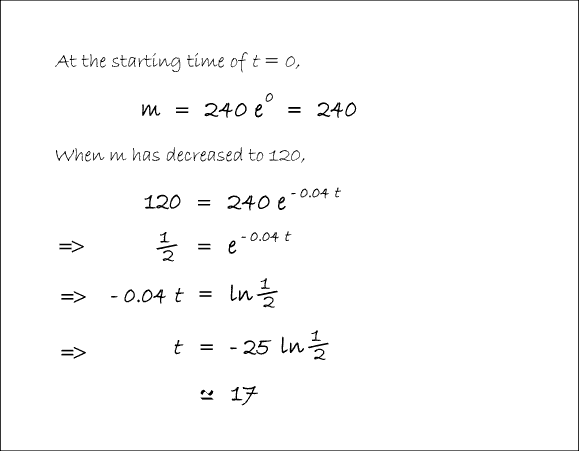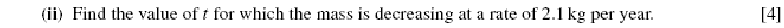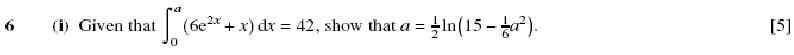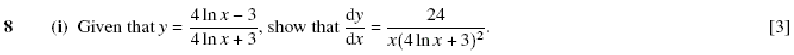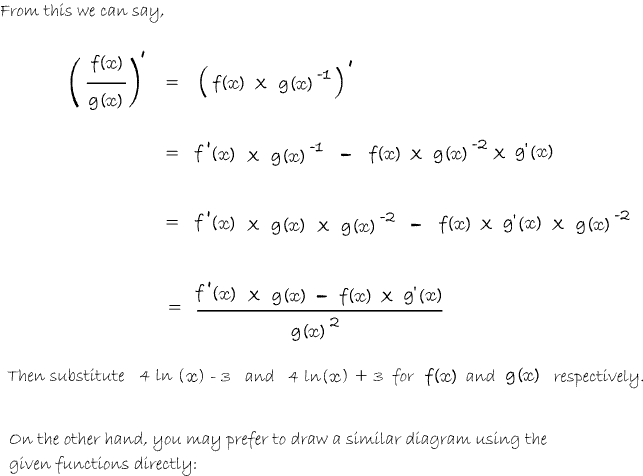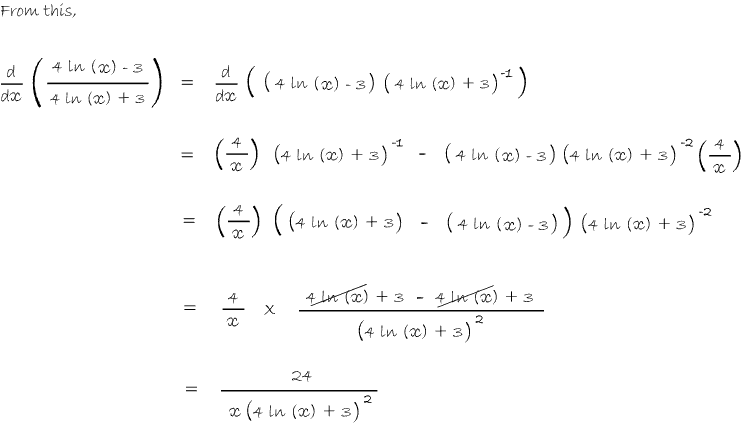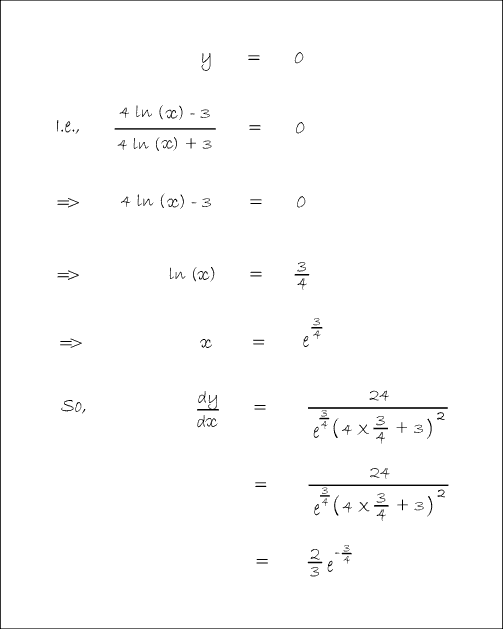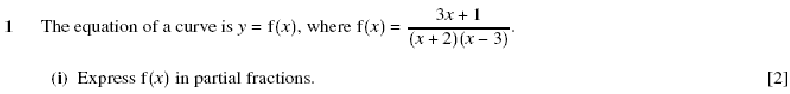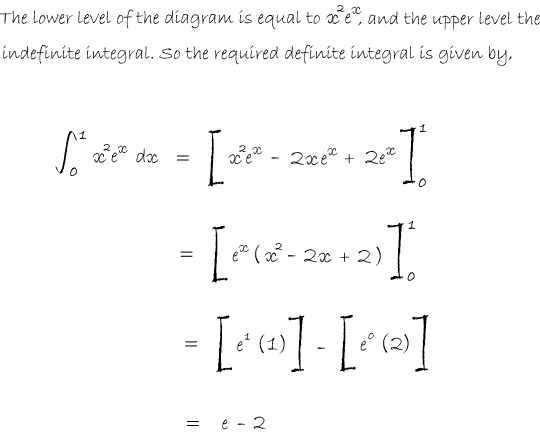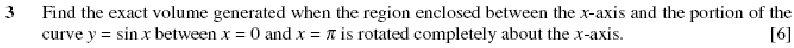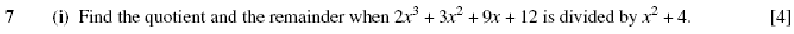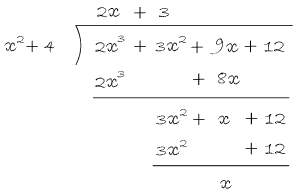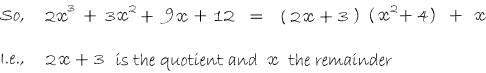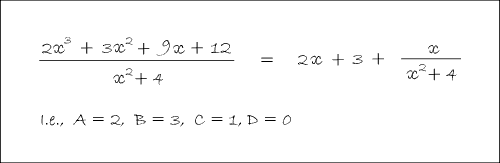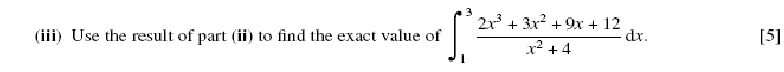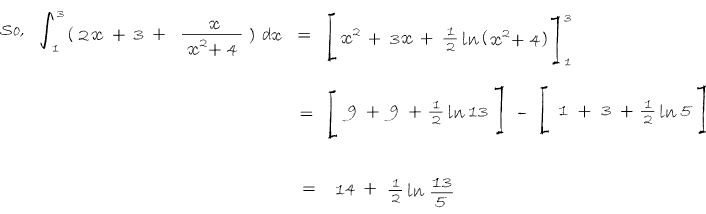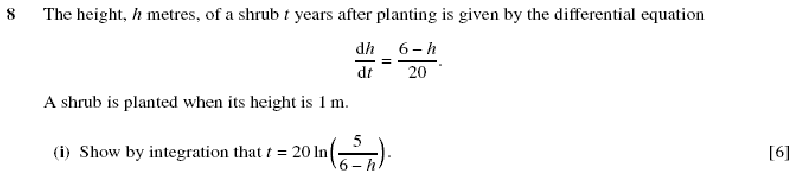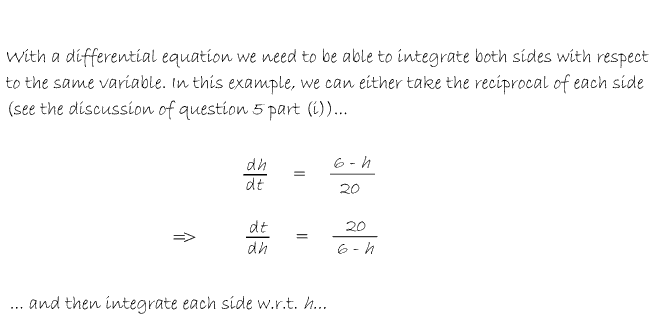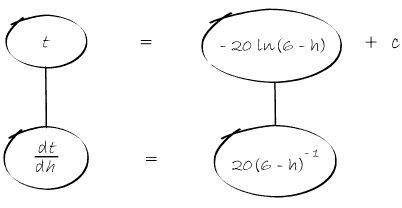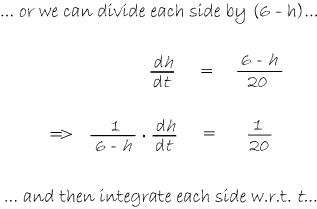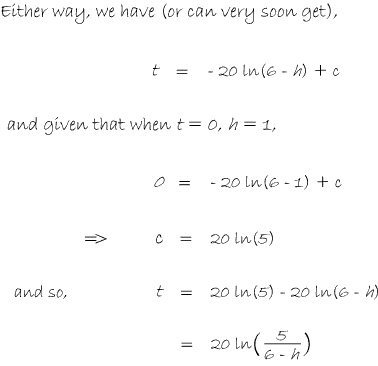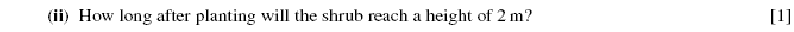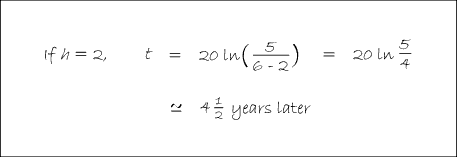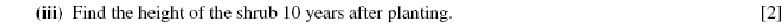In Balloon Calculus, we use three shapes:
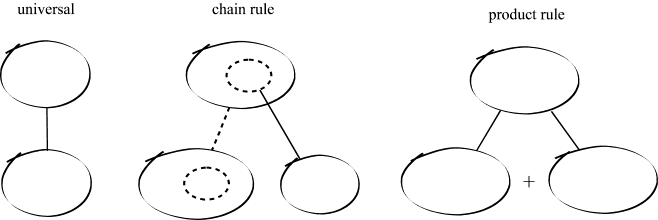
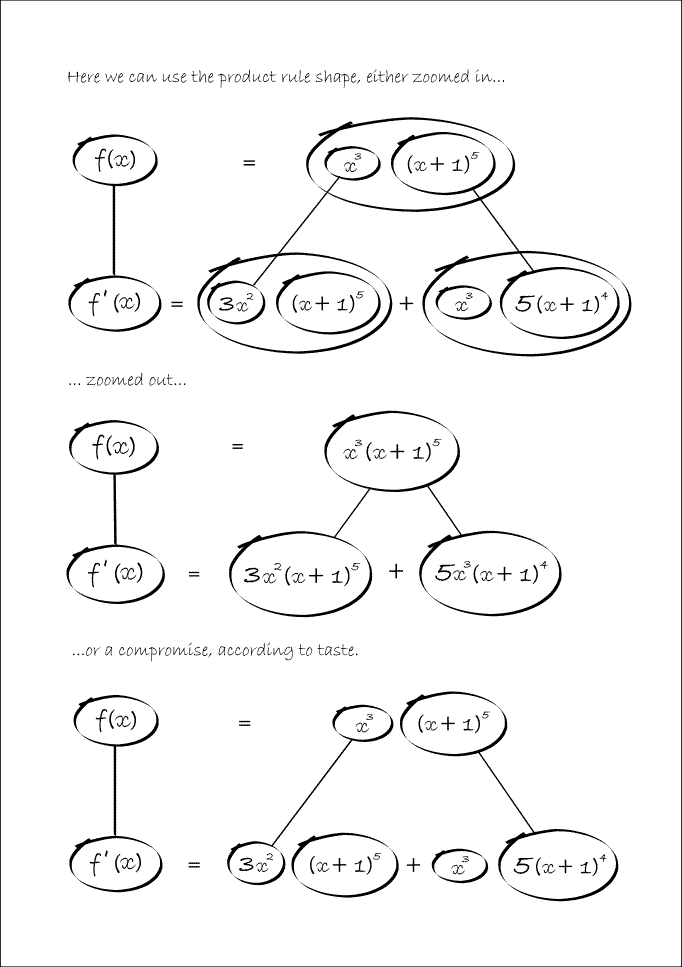
A continuous straight line differentiates going down, integrates going up. The dashed/dotted straight line (in the chain-rule shape) is similar, except that the differentiation or integration is 'with respect to' the expression in the dashed/dotted balloon. The product-rule shape is different, in that the two lines in the zoomed-out version of this shape don't operate independently, but only so as to emphasise the second assumption...
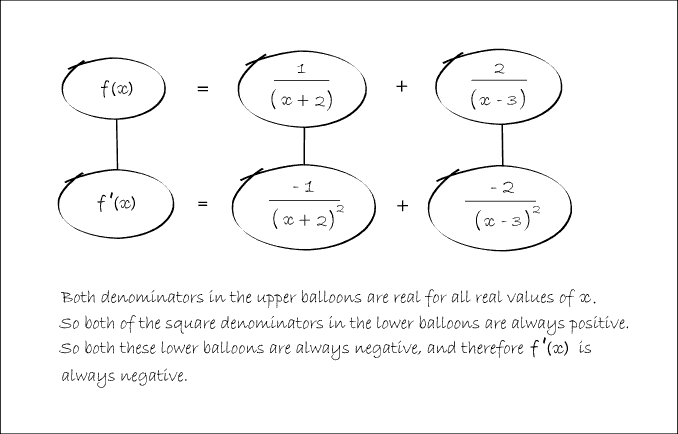
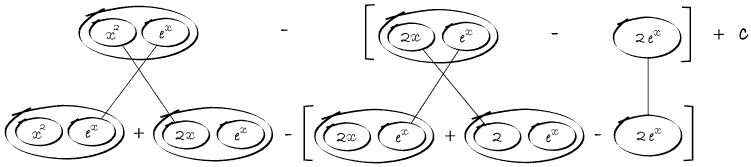
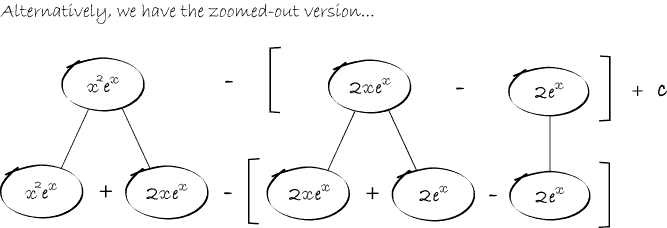
In any shape, the whole of the lower level is the derivative of the whole of the top (i.e. the top is integral of the bottom).