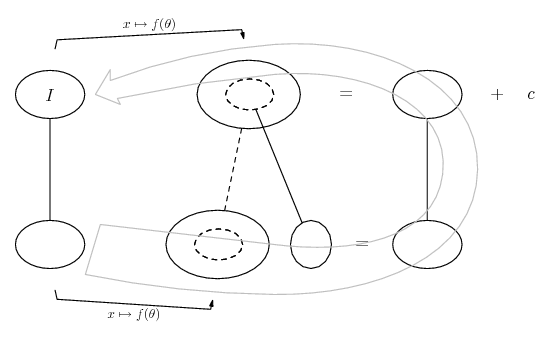
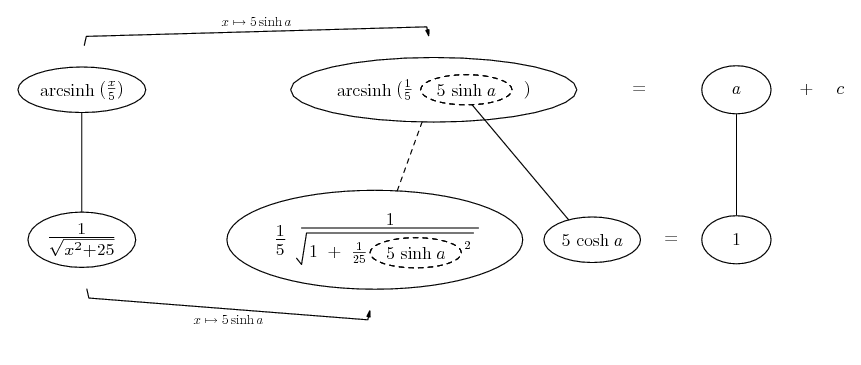
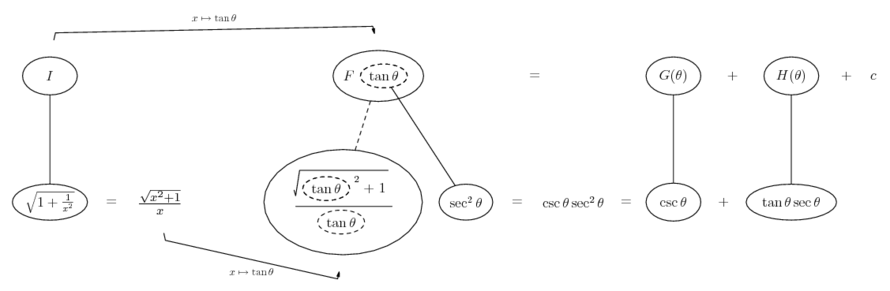
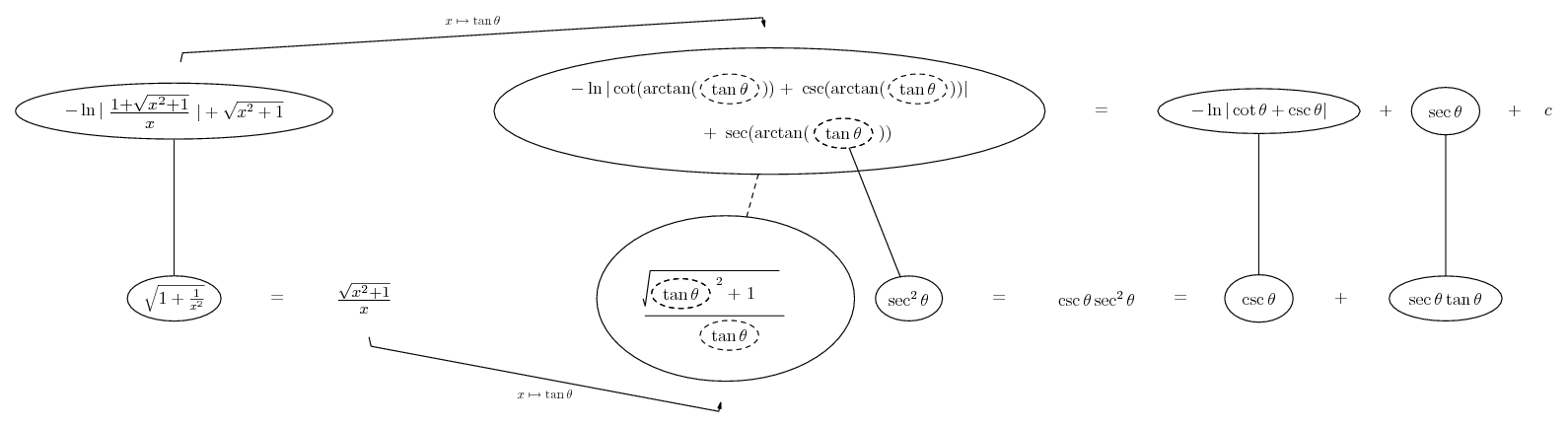
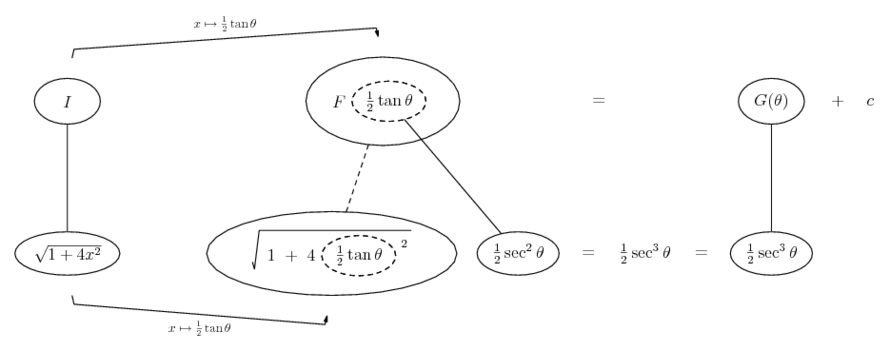
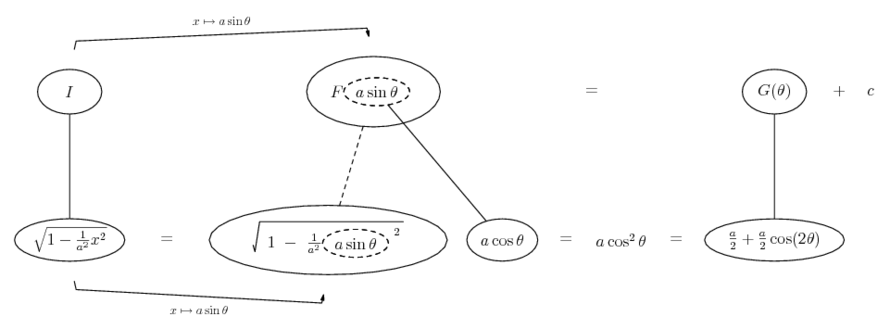
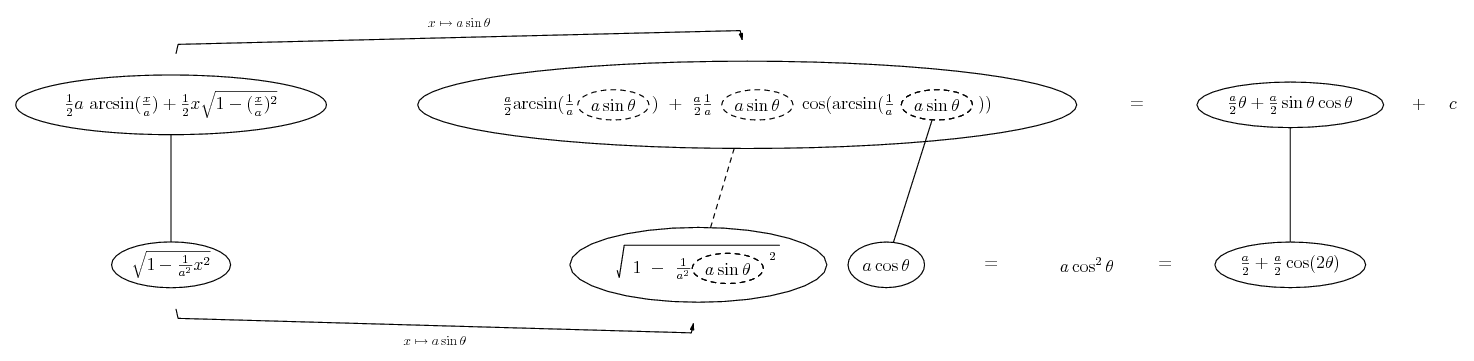
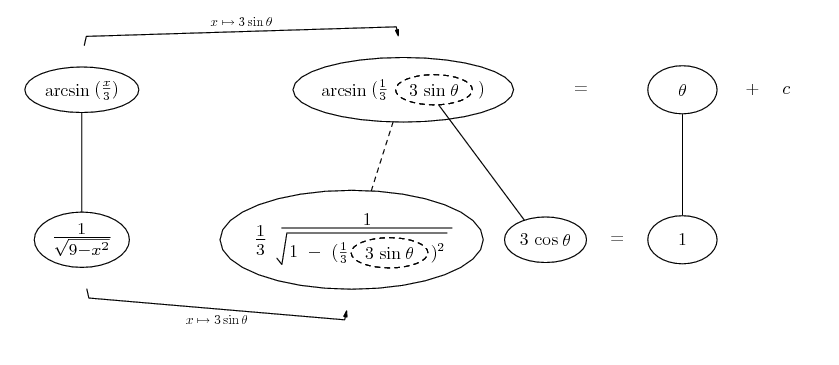
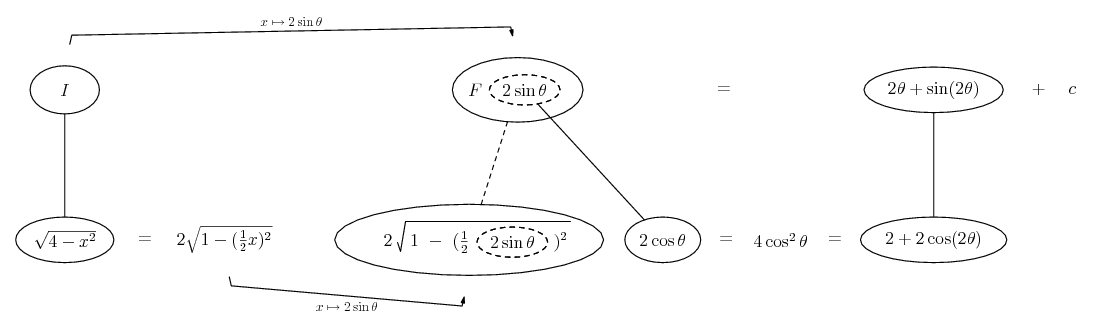
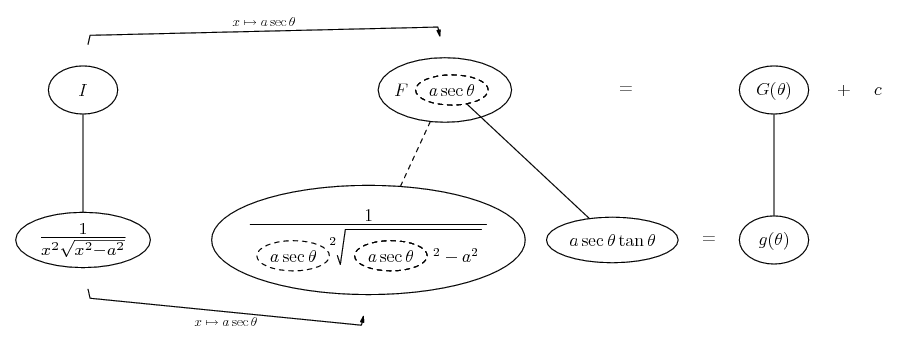
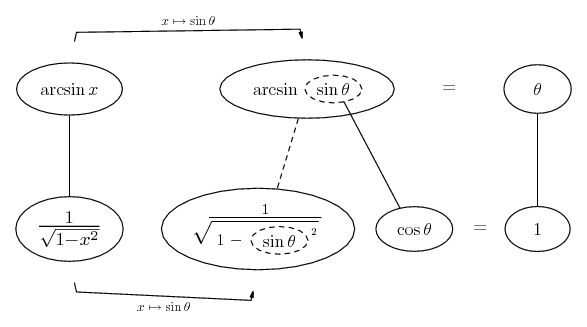
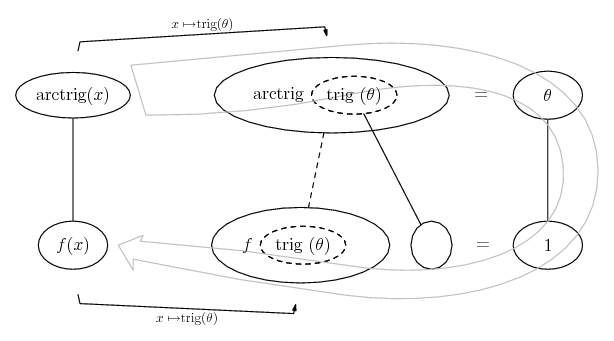
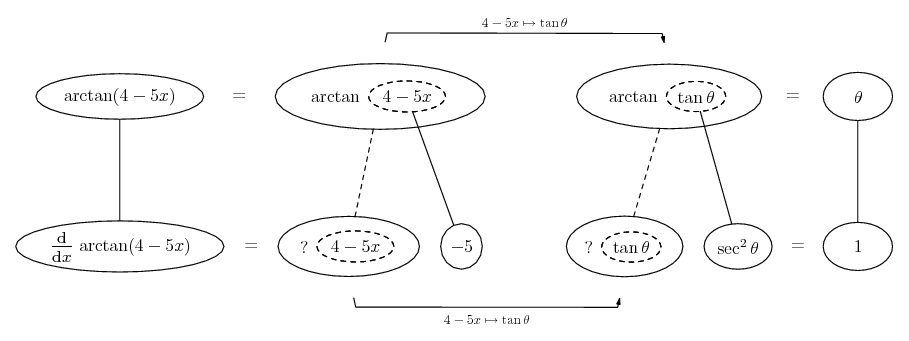
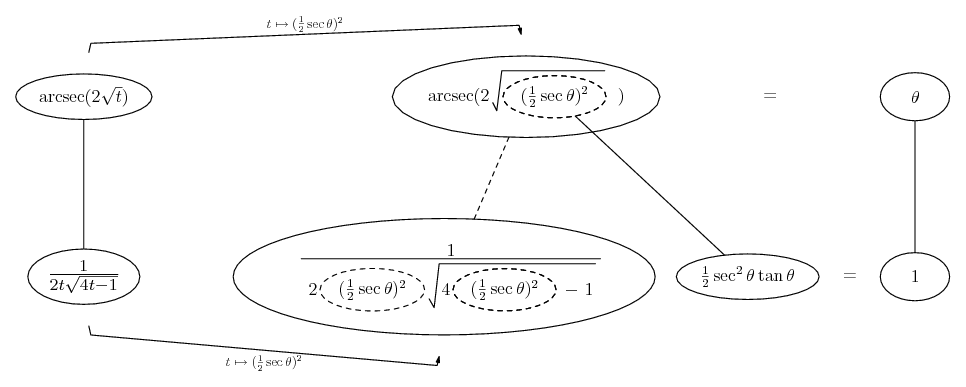
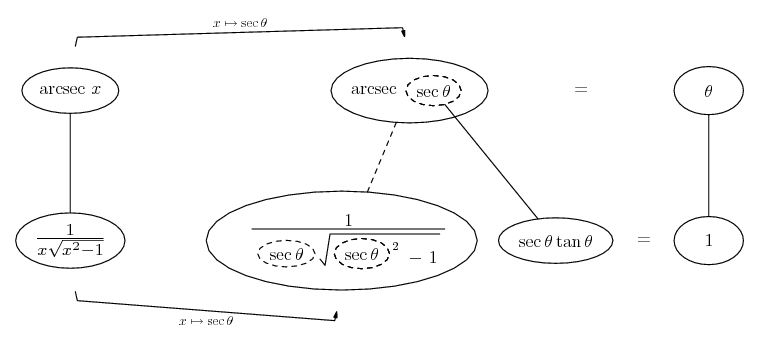
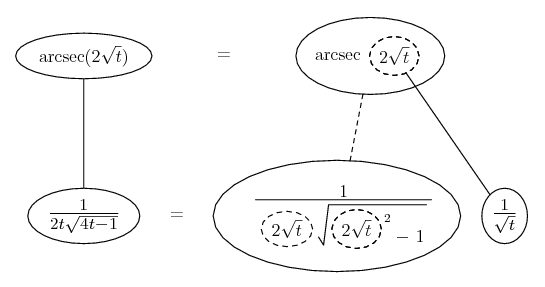
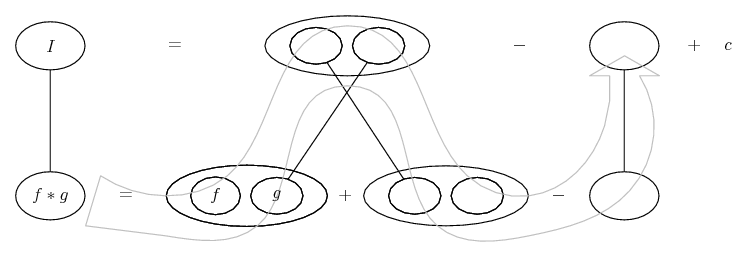
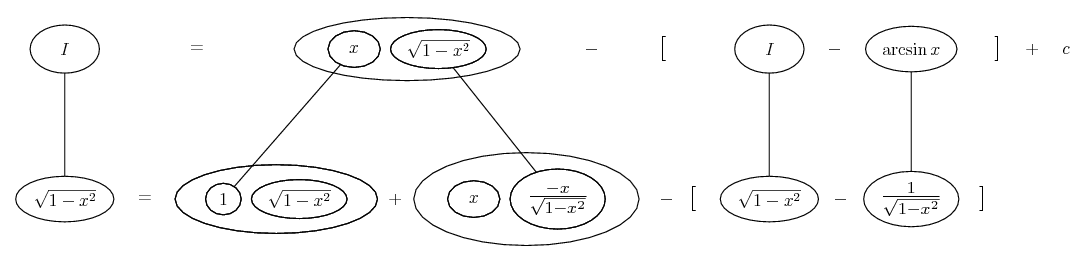
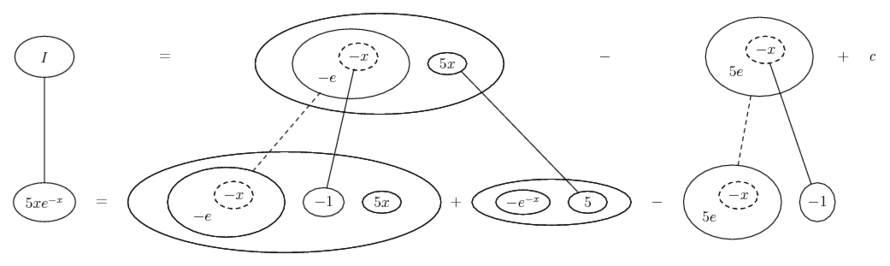
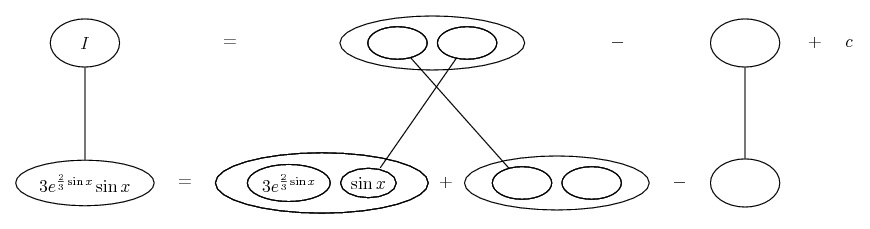
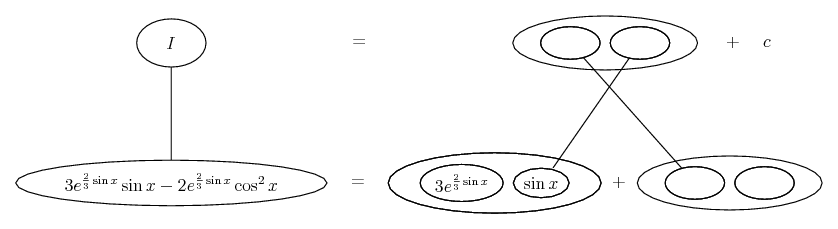
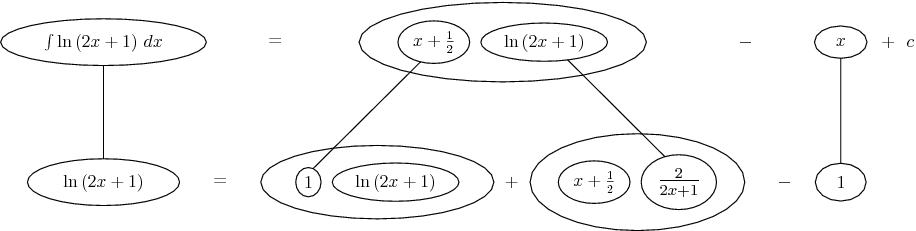
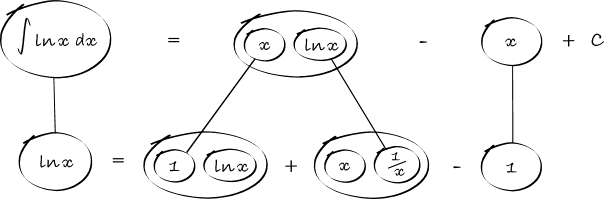
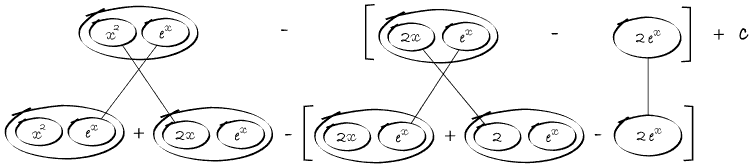
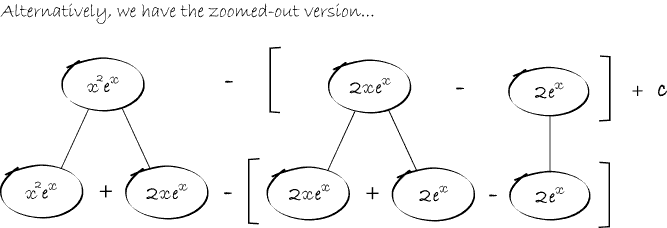
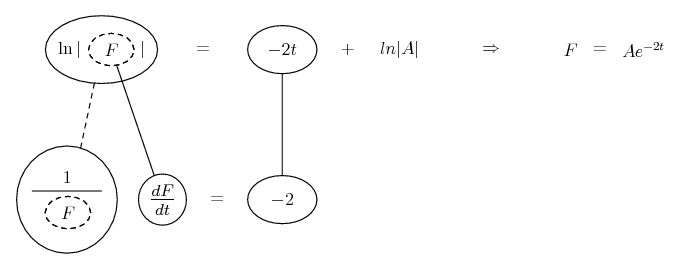
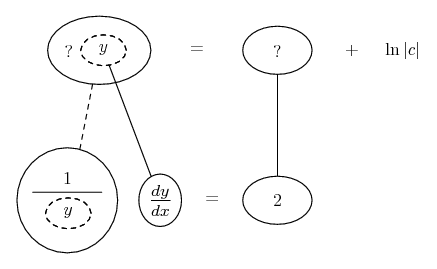
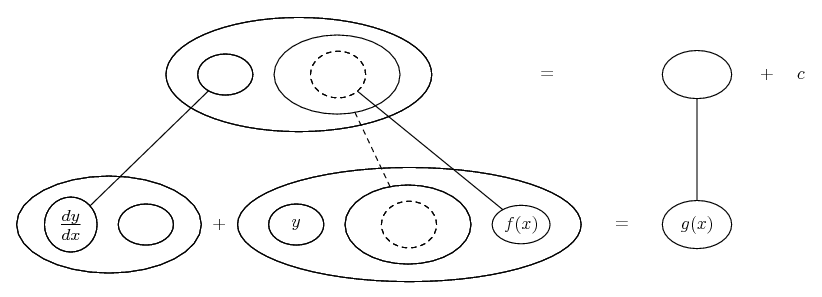
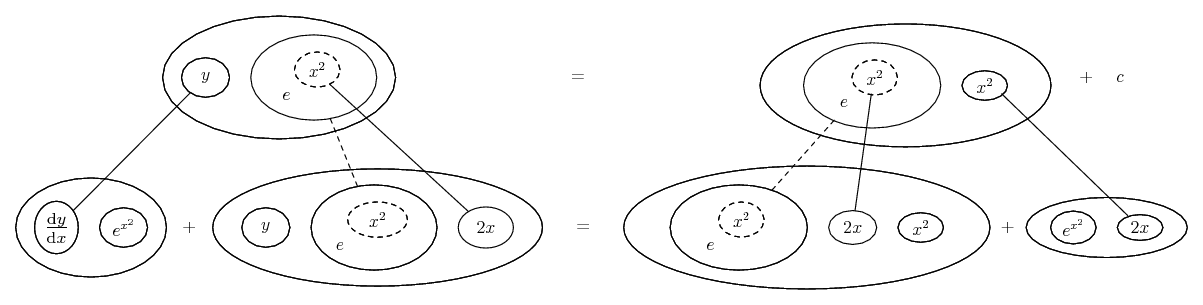
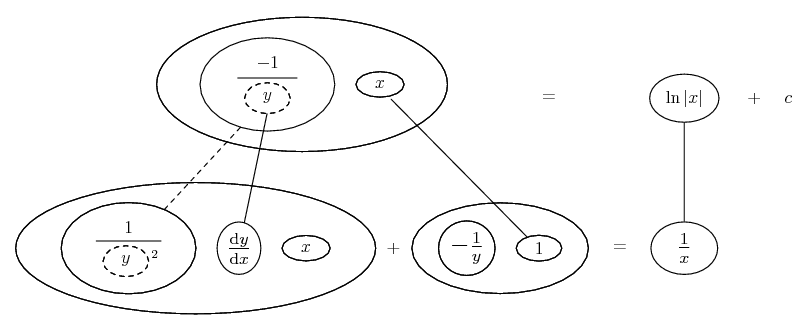
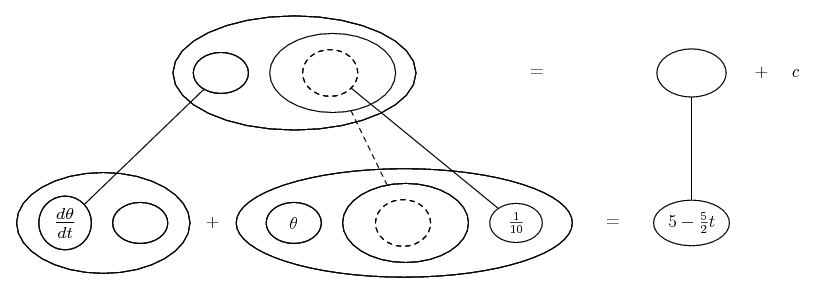
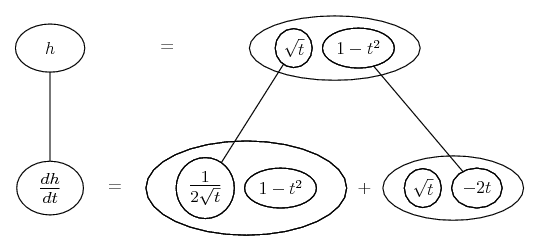
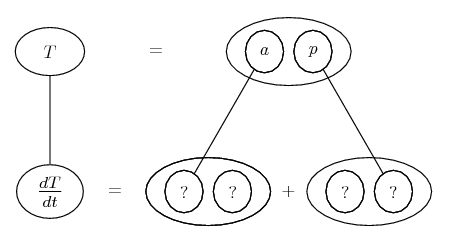
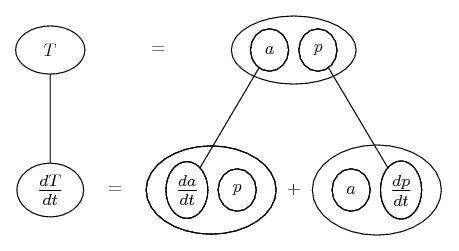
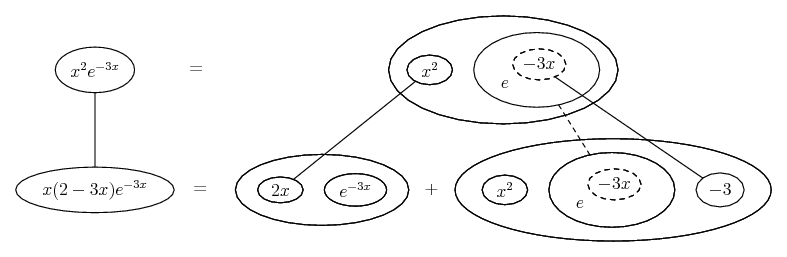
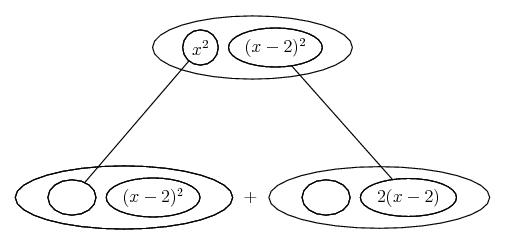
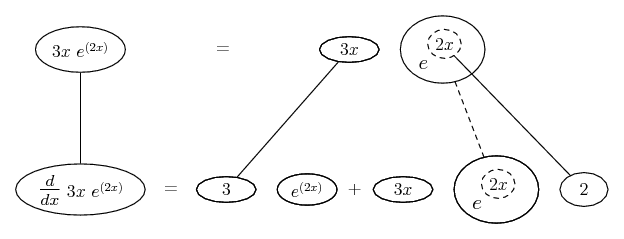
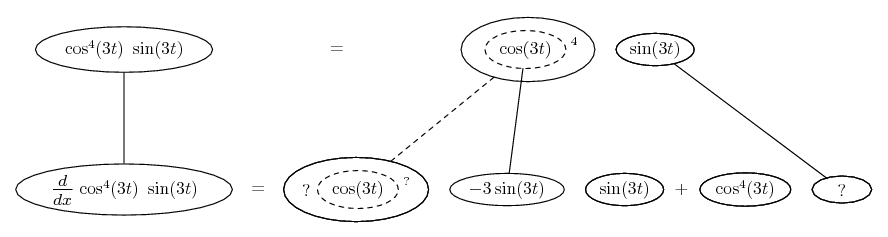
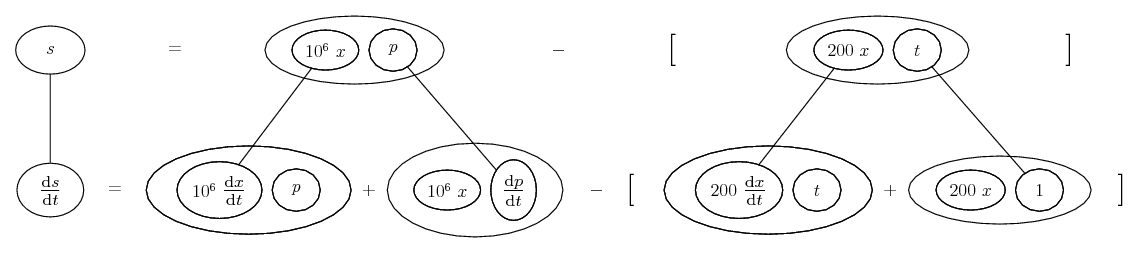
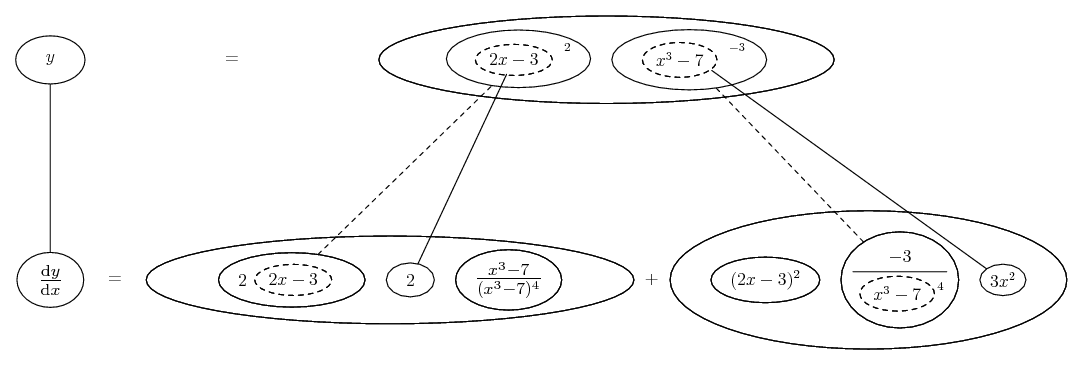
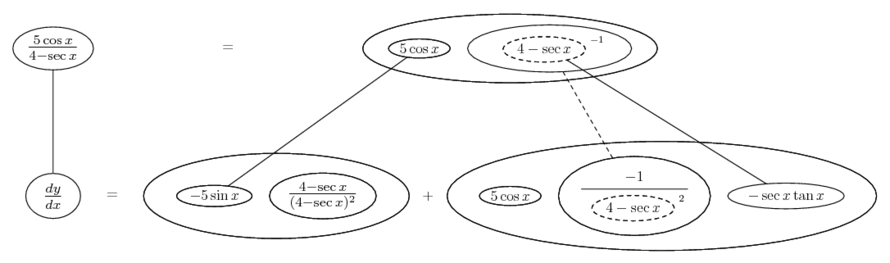
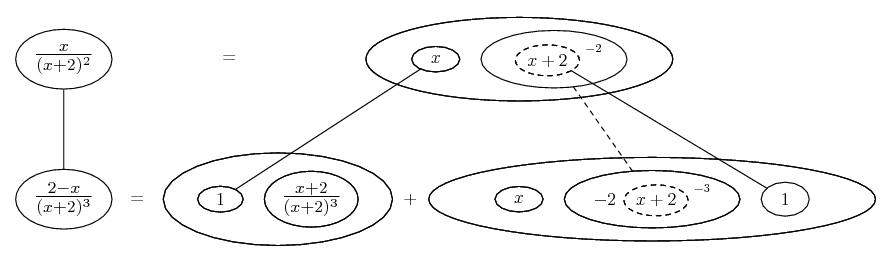
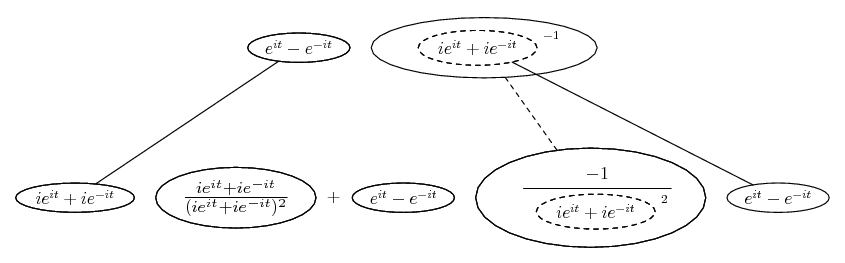
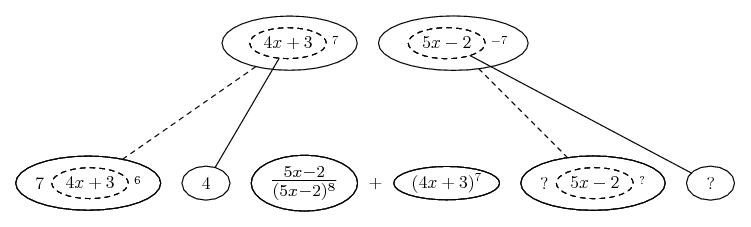
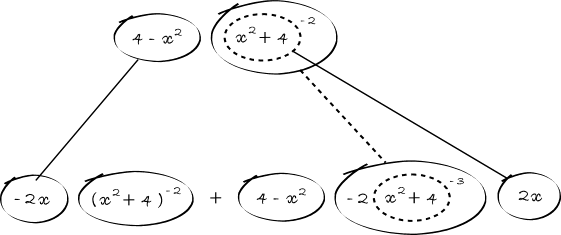
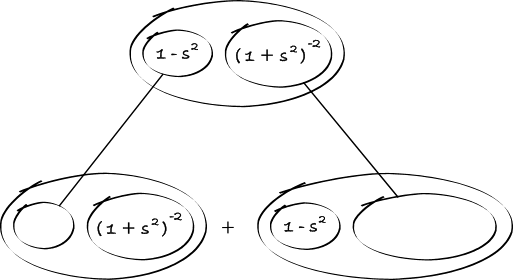
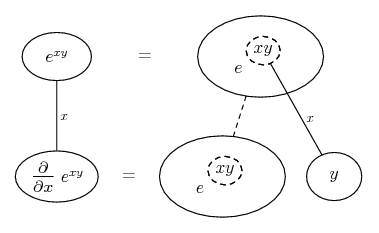
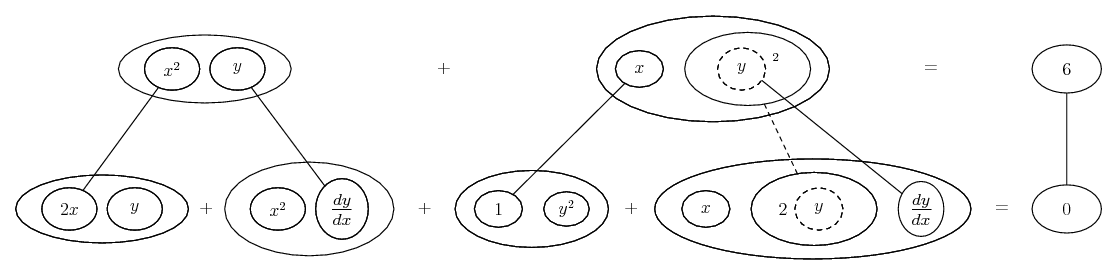
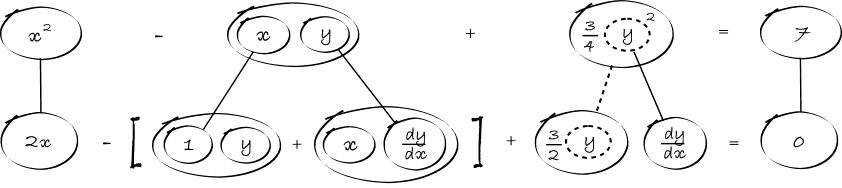
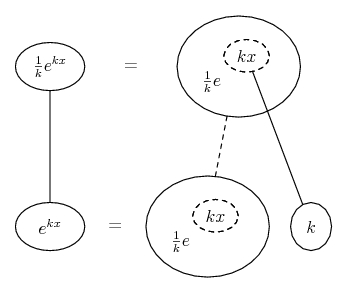
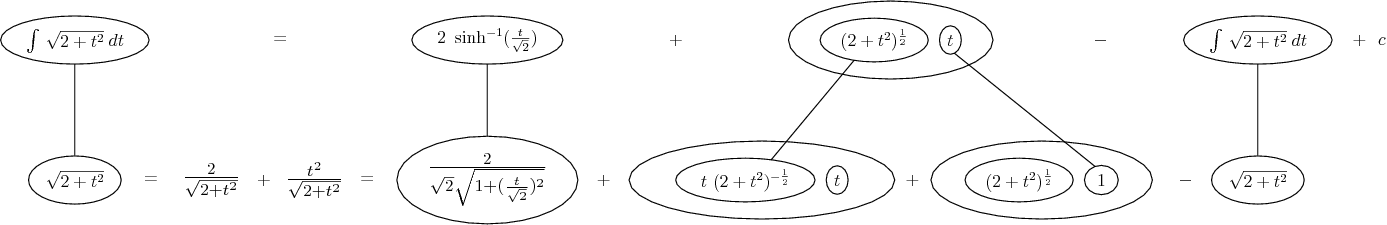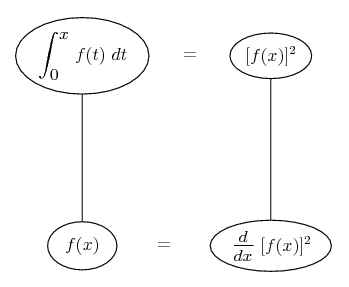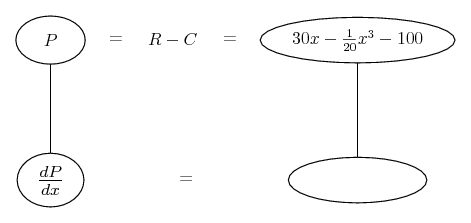Differentiate a product
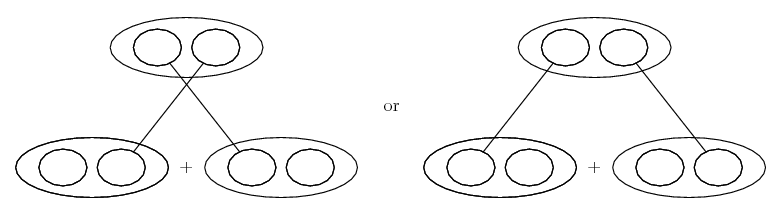
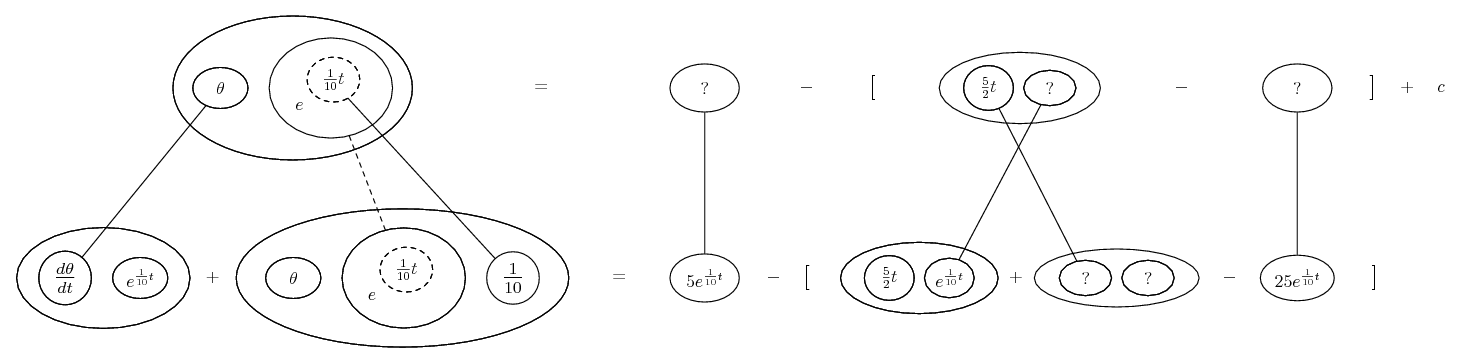
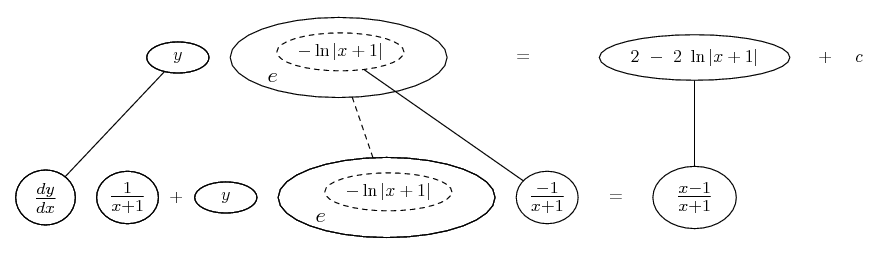
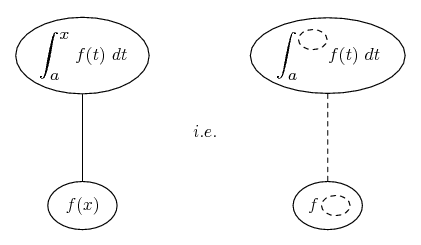
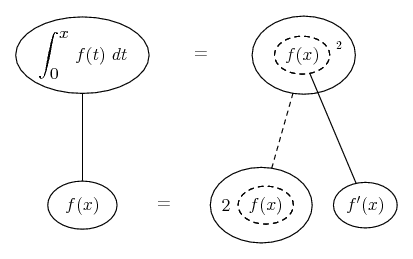
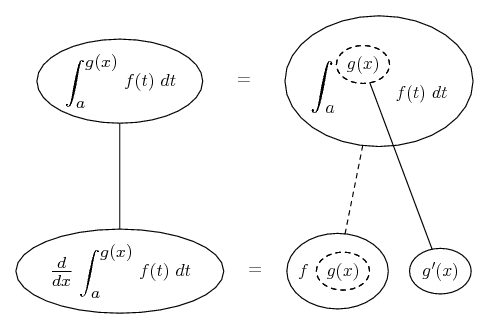
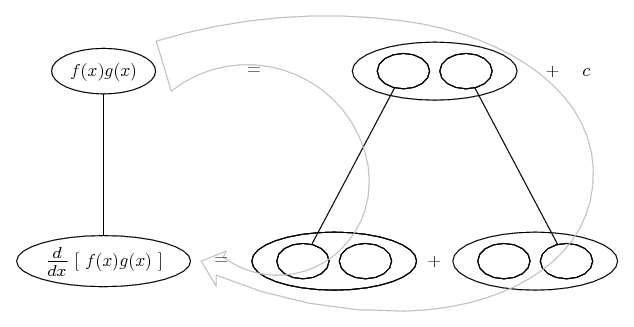
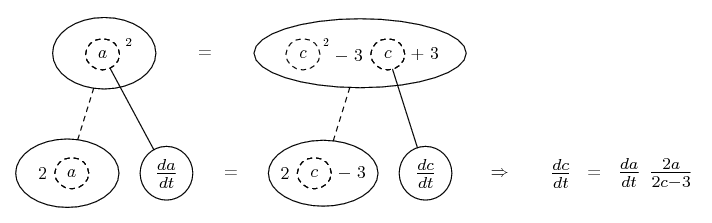
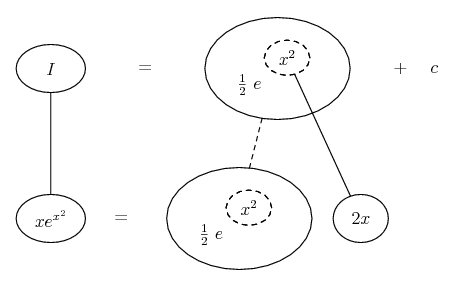
... is the product rule. The straight lines differentiate downwards (integrate up) with respect to x (or whatever the main, explicit variable). And then, because of the product rule, the whole of the bottom row is the derivative (with respect to x) of the whole of the top row. Choosing legs crossed or uncrossed is unimportant when differentiating but crucial for integration by parts.
So differentiation is a downwards journey, and if you want to expand the picture with equals signs (often a good idea) then it's probably also clockwise...
So differentiation is a downwards journey, and if you want to expand the picture with equals signs (often a good idea) then it's probably also clockwise...
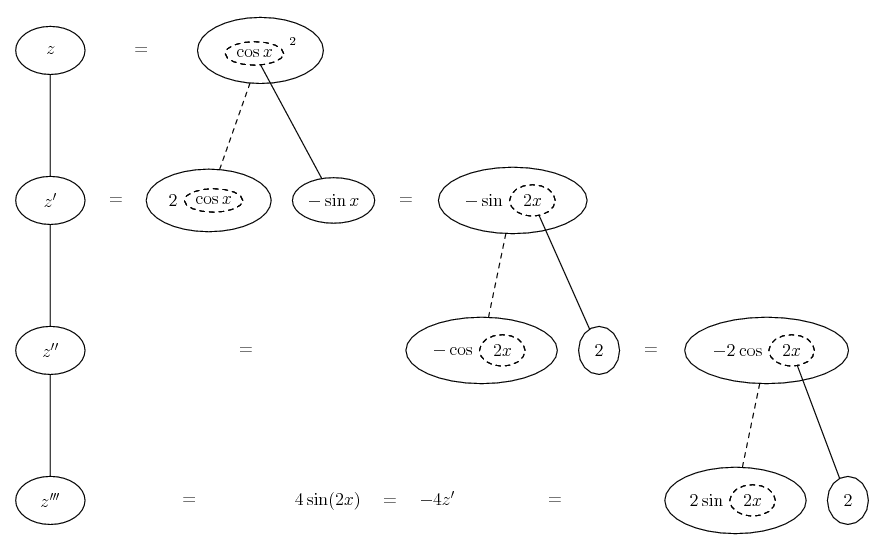
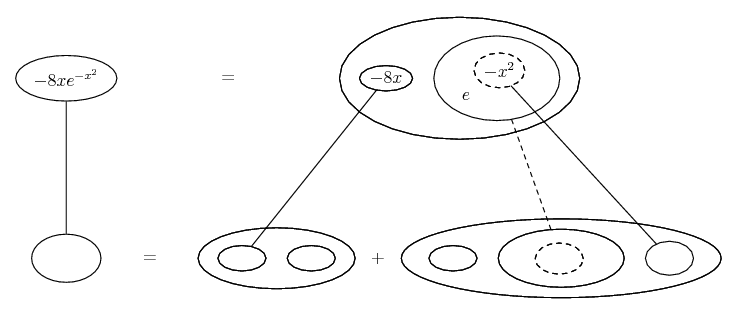
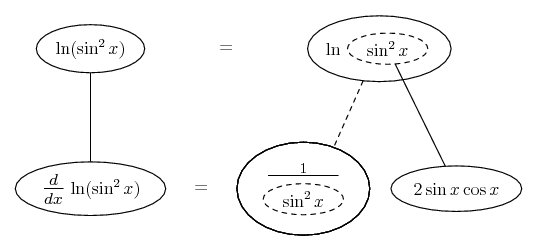
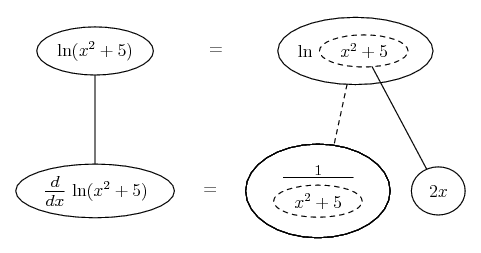
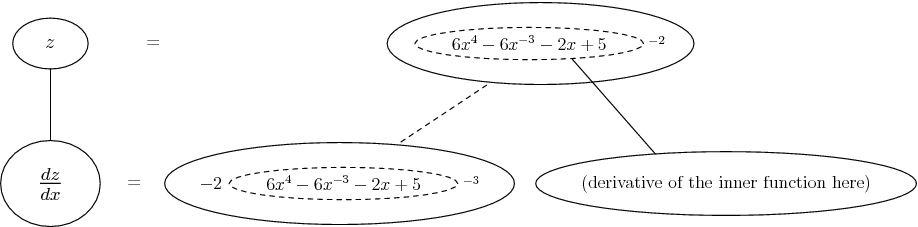
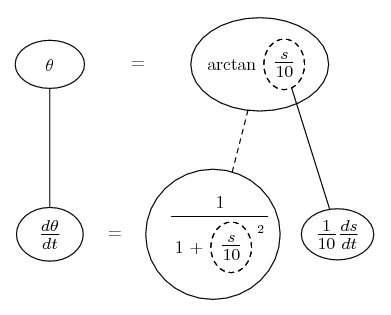
Some of the following examples have the chain rule wrapped inside the product rule...



















![differentiate [ sin( 1 + { cos( 1 + [tan(1 + x)]^4 ) }^3 ) ]^2](/asy/diffChain/nesty4.png)
![differentiate [(4x + 3) / (5x - 2)]^7](/asy/diffProd/quotient3.png)


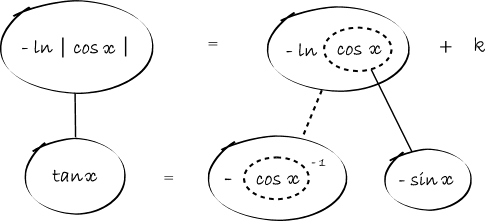

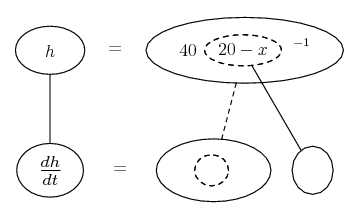
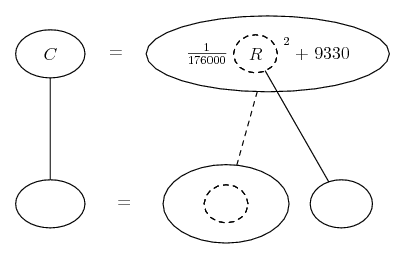

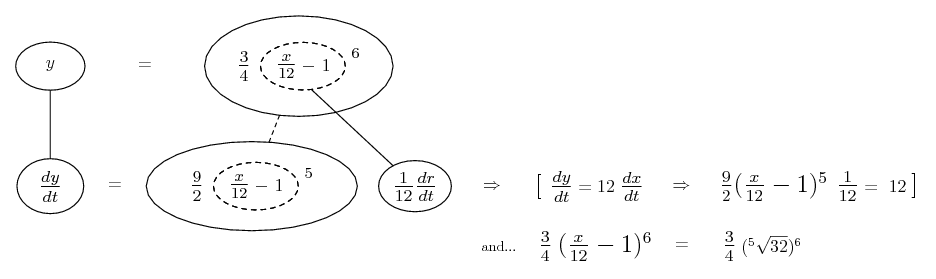











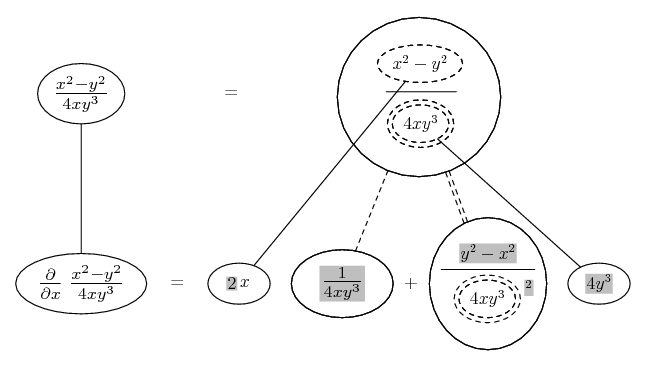
![d/dx [f(x)]^[g(x)]](/asy/diffMulti/mistake.png)


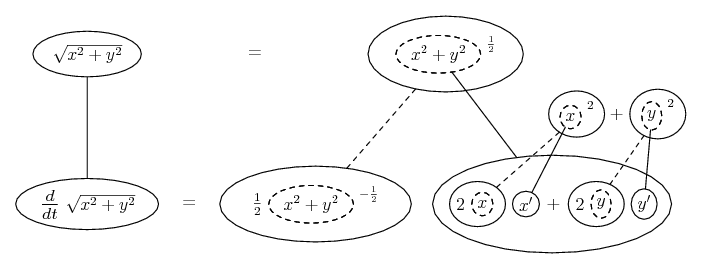




















![integrate 1 / [x (1 - x^(1/4))]](/asy/intChain/uRoot.png)